Respuesta :

Matheng
The vertex of the graph y=|x| is at (0,0)

After transformation the vertex becomes at (-3,-2)
Apply axes transformation from (0,0) to (h,k)
So, the transformation rule is (x,y) → (x-h, y-k)
(h,k) will be equal (-3,-2)


∴ y=|x| ⇒ (y-(-2)) = |x-(-3)|
∴(y+2) = |x+3|
∴ y = |x+3|-2


So, the correct answer is option 2
calculista

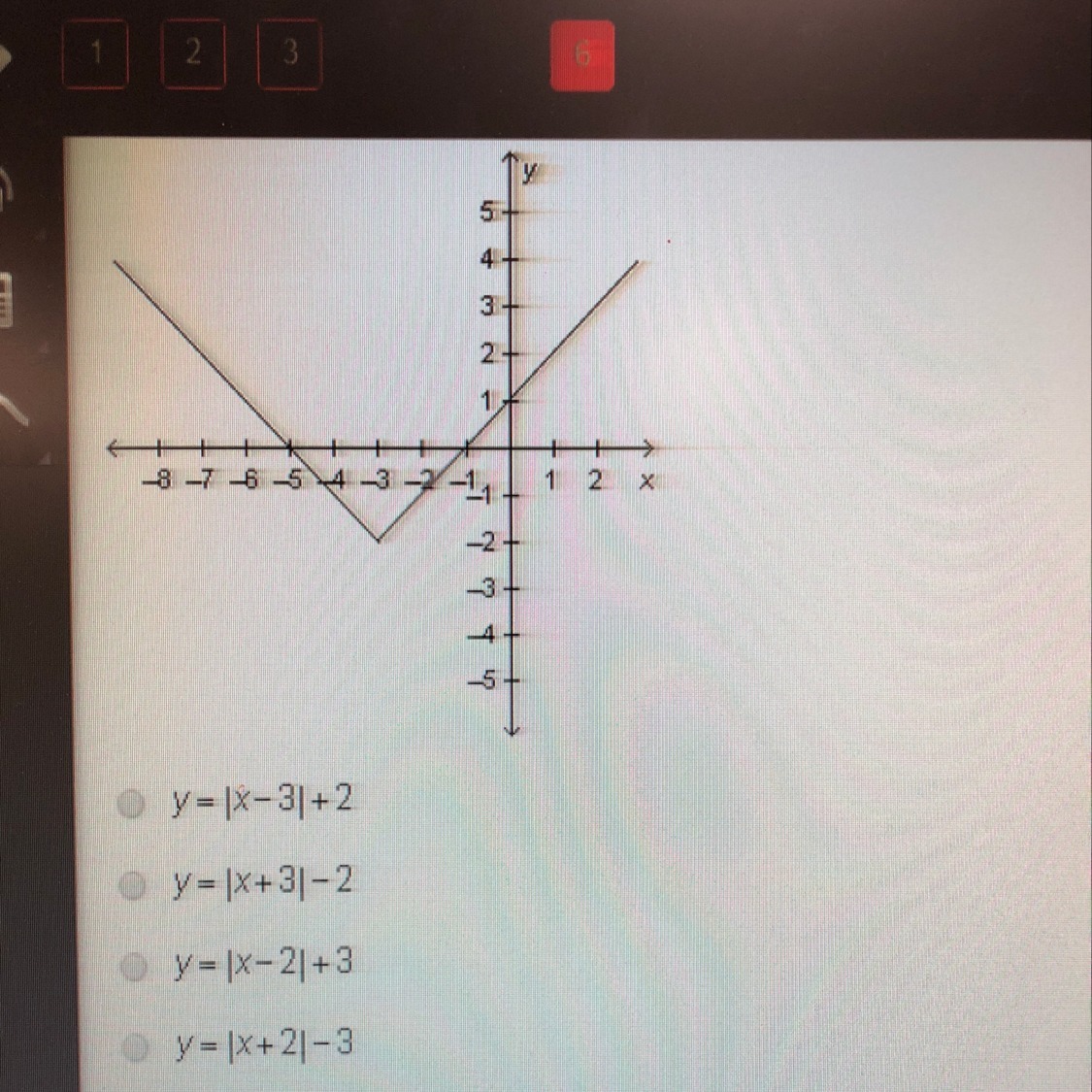
we have that

the original function [tex]y=\left|x\right|[/tex] has the vertex at point [tex](0,0)[/tex]

The transformed function has the vertex at point [tex](-3,-2)[/tex]

so

the rule of the translation is equal to

[tex](x,y)------> (x-3,y-2)[/tex]

That means

The translation is [tex]3[/tex] units to the left and [tex]2[/tex] units down

therefore

the answer is

the transformed function is [tex]y=\left|x+3\right|-2[/tex]



Otras preguntas